Papier im DIN-Format: mehr als nur ein Mathematikfetisch?

210 mal 297 Millimeter – diese Zahlen klingen so beliebig, als hätte sie jemand ausgewürfelt, aber sie definieren jene Papiergröße, die wir im größten Teil der Welt am häufigsten vor uns haben: das DIN-Format A4. Genau genommen gibt es auch eine internationale ISO-Norm und eine österreichische ÖNORM, aber die haben ohnehin nur die deutsche DIN-Norm abgekupfert und bis gerade eben war selbst mir als Österreicher nicht einmal bewusst, dass es diese überhaupt gibt – deshalb nenne ich diese Standards einfach DIN-Format.
Natürlich wurden die A4-Abmessungen nicht durch eine Runde Würfelpoker festgelegt. Ausgangsformat ist die Papiergröße A0, die auf den ersten Blick genauso unrunde Seitenmaße hat; was allerdings fixiert wurde, war einerseits das Verhältnis zwischen Breite und Höhe und andererseits die Fläche.
Das Seitenverhältnis wurde – etwas kryptisch anmutend – mit 1:√2 vorgegeben, das heißt: Wenn ein Blatt einen Meter breit wäre, müsste die Länge √2 (also rund 1,41) Meter betragen. Deutlich eingängiger ist die definierte Fläche: Diese soll für ein Blatt genau einen Quadratmeter betragen. Aus dieser Fläche und dem Seitenverhältnis ergeben sich die konkreten Abmessungen für das Format A0 … und wenn man so ein Blatt vier mal faltet, kommt schließlich das alltagstaugliche A4-Format dabei heraus.
Damit bleibt die Frage, ob der Quadratmeter und die Zweierwurzel sinnvolle Vorgaben sind oder bloß übereifrige Mathematiker befriedigen sollen, denen zwei einfache Längenmaße zu trivial gewesen wären.
Der Meter als Maß aller Dinge
Beginnen wir mit der Fläche: Wenn man, warum auch immer, eine Fläche als Grundmaß für Papierbögen definieren will, dann ist ein Quadratmeter rein formal sicher die naheliegende Wahl, schließlich ist das in unserem metrischen System die Grundeinheit für Flächen im Allgemeinen. US-Amerikaner, die statt des metrischen Systems lieber Füße (foot) und Höfe (yard) als Längeneinheiten verwenden, sehen das vielleicht anders, aber die haben ohnehin auch unsere Papierformate verschmäht.
Während die Wahl der konkreten Fläche grundsätzlich logisch ist, kann man hinterfragen, warum der Referenzwert überhaupt eine Fläche sein muss. Wenn man sich schon am Meter orientiert, hätte man sich das Quadrat schließlich sparen können, indem man mindestens eine der beiden Seiten mit genau einem Meter Länge festgelegt hätte.
Ein Argument für die Flächendefinition ist die Berechnung des Papiergewichtes: Weil dieses üblicherweise in Gramm je Quadratmeter angegeben wird, kann man durch die Flächendefinition relativ einfach ausrechnen, was eine gewisse Menge Papier auf die Waage bringt. Ein einzelner A0-Bogen hat exakt das angegebene Papiergewicht, ein A4-Bogen ein Sechzehntel davon.

Allerdings bin ich als Endnutzer noch nie in die Verlegenheit gekommen, mit dem Gewicht von Papier herumzurechnen. Da war für mich vorher sogar noch das Volumen interessanter, um zu klären, wie viel Papier in eine Badewanne passt. Selbst wenn sich in meinem früheren Büro-Umfeld jemand für das Gewicht interessiert hätte, um sich keinen Bruch zu heben, hätte derjenige höchstwahrscheinlich herumprobiert, geschätzt oder gewogen statt sich über die Formatdefinition zu informieren. Die wenigen Branchen, für die regelmäßige Papiergewicht-Zahlenjongliererei wichtig ist, brauchen die Rechenvereinfachung wahrscheinlich gar nicht, weil dort heutzutage ohnehin alles von Computern kalkuliert wird.
Viel häufiger teile ich in der Praxis Papier in mehrere Segmente, um zum Beispiel eine Tabelle zu erstellen, oder ich muss abschätzen, in welchem Maßstab eine Zeichnung auf ein Blatt passen könnte. Für solche Aufgaben wären eingängige Längenmaße wesentlich nützlicher als eine eingängige Fläche.
Und natürlich wäre es auch auch intuitiver, würde sich das Referenzmaß auf die Papiergröße beziehen, die man tatsächlich ständig verwendet. Verträge und Formulare druckt kaum jemand auf A0-Plakate, schließlich hat außer Putin kaum jemand den passenden Tisch dafür und als Wandzierde machen sie sich auch nicht sonderlich gut.

Würden wir das Alltagsformat A4 mit 210 × 297 Millimetern als Basis für das Ausgangsformat hernehmen und auf glatte 200 × 300 Millimeter runden, hätte eine Seite einen Umfang von genau einem Meter und würde damit auch gut ins metrische System passen.
Ein Seitenverhältnis für alle
Eine Abmessung von glatten 200 × 300 Millimetern entspricht – wenig überraschend – einem Seitenverhältnis von 2:3. Laut Wikipedia war das damals tatsächlich eine übliche Relation. Wenn man einen Papierbogen mit solchen Abmessungen der Länge nach in der Mitte zusammenfaltet, hat dieses kleinere Format allerdings ein anderes, ebenfalls vormals gebräuchliches Seitenverhältnis, nämlich 3:4. Mit jeder weiteren Faltung wechselt man zwischen diesen beiden Verhältnissen.
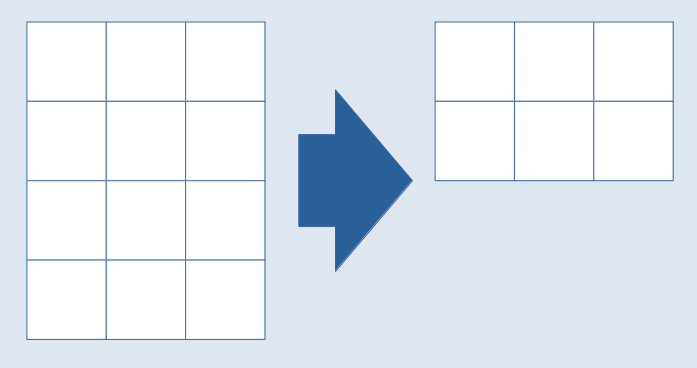
Will man stattdessen, dass es sich beim Falten nicht ändert, gibt es nur ein einziges zulässiges Seitenverhältnis … und offenbar will man das, denn genau dieses Verhältnis wurde in der DIN-Norm festgeschrieben: 1:√2.
Glatte Werte für Länge und Breite kann man sich damit in die Haare schmieren, denn die Wurzel aus 2 ist genauso wie die Kreiszahl Pi eine irrationale Zahl, also so ein Unding, wo nach dem Komma unendlich viele Ziffern folgen, die sich nie wiederholen. Wenn ein Blatt einen Meter breit wäre, müsste es bei diesem Seitenverhältnis theoretisch 1,41421356237… Meter lang sein. Die tatsächlichen DIN-Formate werden deshalb auf ganze Millimeter gerundet; analog zu Pi könnte man das als »Daumen mal √2« bezeichnen.
Im Gegensatz zum A0-Quadratmeter habe ich von diesem Seitenverhältnis schon in der Praxis profitiert. Weil es immer gleich ist, kann ich Dokumente in einem dieser Papierformate bedenkenlos auf ein beliebiges anderes A-Format vergrößern oder verkleinern ohne dass ein unnötiger Rand bleibt oder etwas abgeschnitten wird. So kann ich ohne Umwege aus einem Wurfzettel ein Plakat machen oder zum Papiersparen auf einem einzelnen A4-Blatt zwei Seiten nebeneinander drucken, die eigentlich jede für sich eine A4-Seite wären.
Papier als Augenschmaus?
Dass man bei einem gleichbleibenden Seitenverhältnis seine Inhalte mühelos aufblasen oder schrumpfen kann, ist für Produzenten erfreulich. Die wesentlich wichtigere Frage ist allerdings, ob das Format auch für Konsumenten vorteilhaft ist, andernfalls produziert man in seiner voreiligen Begeisterung etwas, was sich Endnutzer mangels Benutzbarkeit bestenfalls zum Anschauen an die Wand nageln können – und das ist selbst im Fall von Papier nur relativ selten der angestrebte Anwendungsfall.
Weil die DIN-Papierformate unlängst ihr 100-jähriges Jubiläum hatten, konnte ich dazu ein paar spannende, schriftliche Diskussionen verfolgen. Allerdings ließ die Spannung deutlich nach, als mir bewusst wurde, dass die meisten Diskutanten dem Papierformat fast schon magische Eigenschaften zuschrieben. Da wurde über die Lesbarkeit von Text philosophiert, als würden typographische Eigenschaften wie Schriftart, Schriftgröße und Weißraum keine Rolle spielen; dabei ist genau das Gegenteil der Fall: Solange ein Blatt nicht zu klein ist, kann ich Text in jeder beliebigen Form darauf unterbringen. Auf meinen Computermonitoren habe ich ja üblicherweise auch trotz Breitbildformat keine unleserlich langen Zeilen vor mir.

Selbst zu fixen Schrifteigenschaften könnte man nur schwer das optimale Papierformat finden, da die Wahrnehmung sehr vom Anwendungsfall und von persönlichen Anforderungen abhängt. Dasselbe Blatt Papier wirkt ganz anders, je nachdem, ob man es unter künstlichem Licht knapp vor der Nase oder im Halbschatten im ausgestreckten Arm hält. Für mich als kurzsichtigen Stubenhocker ist das erste Szenario wesentlich realistischer als das zweite – für einen weitsichtigen Naturburschen ist wahrscheinlich das Gegenteil der Fall.
Was mitunter auch diskutiert wird, ist die Ästhetik. Da wird es natürlich erst recht subjektiv und vielleicht sogar ein wenig esoterisch, aber wenn man diesen Hexenkram trotzdem irgendwie messen will, dann wäre es naheliegend, den Goldenen Schnitt als Maßstab heranzuziehen; das ist ein Verhältnis von zwei Strecken, das gerne als besonders harmonisch bezeichnet wird. Beim Goldenen Schnitt ist die längere Seite 1,62-mal länger als die kürzere.
| Verhältnis | Faktor der längeren Seite |
|---|---|
| Goldener Schnitt | 1,62 |
| 2:3 | 1,50 |
| 1:√2 | 1,41 |
| 3:4 | 1,33 |
Das Verhältnis von 1:√2 wäre dementsprechend näher an diesem Optimum als es das althergebrachte Format 3:4 ist. Die ebenfalls klassische Relation 2:3 wäre allerdings noch näher dran.
Handlich in der Handhabung?
Genauso wie die optische Wahrnehmung ist auch die physische Handhabung vom Anwendungsfall und der Person abhängig. Mit Wurstfingern auf der Baustelle fühlt sich ein und dasselbe Papierformat wahrscheinlich anders an als mit Spaghettifingern im Büro.
Wie schon beim Visuellen ist es weniger das Seitenverhältnis als vielmehr die Größe, die den Unterschied macht. Und hier habe ich in den Diskussionen einen durchaus interessanten Denkanstoß gefunden: Für Bücher sei A4 zu groß, A5 aber zu klein. Man kann sicher trefflich darüber streiten, inwiefern diese konkrete Beschwerde wirklich zutrifft, aber eines ist Fakt: An alltagstauglichen Größen bieten die A-Formate verdammt wenig Auswahl.
Ganze elf Klassen sind in der A-Reihe spezifiziert – von A0 bis A10. Aber mehr als ein bis zwei davon verwenden die meisten von uns so gut wie nie, weil die jeweilige Verdoppelung von einem Format zum nächstgrößeren einen gewaltigen Sprung darstellt. A3 geht schon als Plakat durch und A6 ist ein Hosentaschenformat. Für persönliche Vorlieben und Anforderungen bleibt da rund um A4 und A5 kein Platz. Im Gegenzug kann man sich aber bei Bürozubehör ungeschaut darauf verlassen, dass es zu den eigenen Unterlagen passt … solange man es nicht aus Ländern importiert, die Füße als Längeneinheiten nutzen.
Kein Standard ohne Ausnahmen
Dass wir in unseren Breiten die A-Maße als Standard verwenden, heißt trotz allem keineswegs, dass diese bei uns alternativlos sind. Ironischerweise herrscht ausgerechnet bei Büchern, Zeitungen und Magazinen bis heute ein Wildwuchs an Formaten, obwohl ein Vorläufer der DIN-Norm ganz konkret dazu gedacht war, den Platzbedarf in Bibliotheken zu optimieren.

Die DIN-Norm selbst beinhaltet neben der A-Reihe auch noch weitere Formate, aber dort wird es rasch inkonsistent und unübersichtlich. So kennt sie neben A auch noch B, C und D, wobei aber B aus irgendeinem Grund das größte Format ist und obendrein das einzige dieser drei zusätzlichen, das auch in der internationalen ISO-Norm existiert.
Insofern bin ich ganz dankbar, mir in meinem Alltag abseits der Bestückung meines Bücherregals keine Gedanken über alternative Formate machen zu müssen. Dort, wo ich meine Regale mit Arbeitsmappen bestücke, funktioniert das dank A4 nach dem Konzept »Tetris für Dummies«.
Artikel-Informationen
Artikel veröffentlicht:
Der monatliche WIESOSO-Artikel per E-Mail
Hat Dir dieser Text gefallen und würdest Du in Zukunft gerne per E-Mail über neue WIESOSO-Artikel auf dem Laufenden bleiben? Dann ist die WIESOSO-E-Mail-Gruppe genau das Richtige für Dich!

Kommentare
Neuen Kommentar schreiben
Bisherige Kommentare